Load carrying capacity and life
- Fatigue theory as a principle
- Dimensioning of rolling bearings
- Dynamic load carrying capacity and life
- Calculation of the rating life
- Basic rating life
- Equivalent dynamic bearing load
- Expanded adjusted rating life
- Requisite minimum load
- Equivalent operating values
- Guide values for dimensioning
- Static load carrying capacity
- Equivalent static bearing load
- Operating life
Load carrying capacity and life
“Expanded calculation of the adjusted rating life”
Schaeffler introduced the “Expanded calculation of the adjusted rating life” in 1997. This method was standardised for the first time in DIN ISO 281 Appendix 1 and has been a constituent part of the international standard ISO 281 since 2007. As part of the international standardisation work, the life adjustment factor aDIN was renamed as aISO but without any change to the calculation method.
Fatigue theory as a principle

The basis of the rating life calculation in accordance with ISO 281 is Lundberg and Palmgren's fatigue theory which always gives a final rating life.
However, modern, high quality bearings can exceed by a considerable margin the values calculated for the basic rating life under favourable operating conditions. Ioannides and Harris have developed a further model for fatigue in rolling contact that expands on the Lundberg and Palmgren theory and gives a better description of the performance capability of modern bearings.
Values which must be taken into account in the “Expanded calculation of the adjusted rating life”
The method “Expanded calculation of the adjusted rating life” takes account of the following influences:
- the bearing load
- the fatigue limit of the material
- the extent to which the surfaces are separated by the lubricant
- the cleanliness in the lubrication gap
- additives in the lubricant
- the internal load distribution and frictional conditions in the bearing
The influencing factors, especially those relating to contamination, are extremely complex. A great deal of experience is essential for an accurate assessment. As a result, please consult Schaeffler for further advice.
The tables and diagrams in this chapter can only give guide values.
Dimensioning of rolling bearings
The required size of a rolling bearing is dependent on the demands made on its:
- rating life
- load carrying capacity
- operational reliability
Dynamic load carrying capacity and life
Basic dynamic load ratings
The dynamic load carrying capacity is described in terms of the basic dynamic load ratings. The basic dynamic load ratings are based on DIN ISO 281.
The basic dynamic load ratings for rolling bearings are matched to empirically proven performance standards published in previous FAG and INA catalogues.
The fatigue behaviour of the material determines the dynamic load carrying capacity of the rolling bearing.
Dynamic load carrying capacity
The dynamic load carrying capacity is described in terms of the basic dynamic load rating and the basic rating life.
Factors influencing the fatigue life
The fatigue life is dependent on:
- the load
- the operating speed
- the statistical probability of the first appearance of failure
Basic dynamic load rating C
The basic dynamic load rating C applies to rotating rolling bearings. It is:
- a constant radial load Cr for radial bearings
- a constant, concentrically acting axial load Ca for axial bearings
The basic dynamic load rating C is that load of constant magnitude and direction which a sufficiently large number of apparently identical bearings can endure for a basic rating life of one million revolutions.
Calculation of the rating life
Calculation methods
The methods for calculating the rating life are:
- basic rating life L10 and L10h to ISO 281 ➤ Equation and ➤ Equation
- expanded adjusted rating life Lnm to ISO 281 ➤ link
Basic rating life
L10 or L10h
The basic rating life in millions of revolutions (L10) is determined in accordance with ➤ Equation, the basic rating life in operating hours (L10h) is determined in accordance with ➤ Equation.
Rating life in revolutions
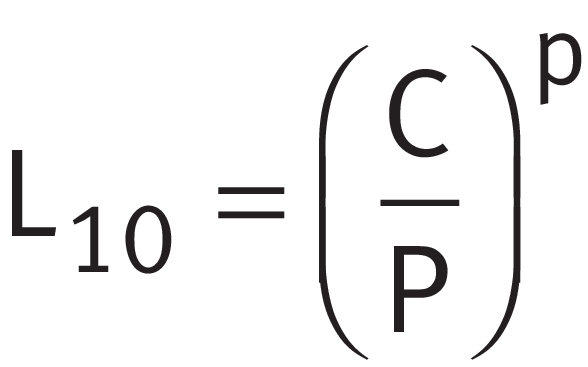
Rating life in operating hours
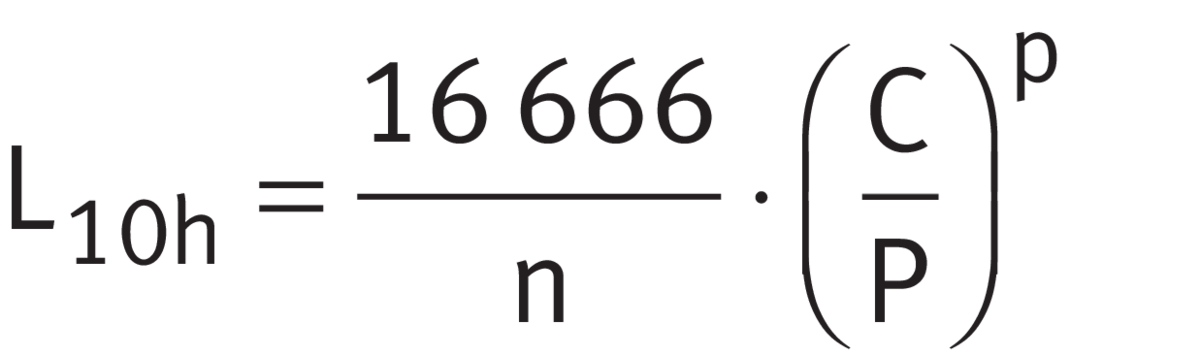
Legend
| L10 | 106 |
The basic rating life in millions of revolutions, that is reached or exceeded by 90% of a sufficiently large number of apparently identical bearings before the first indications of material fatigue appear |
| L10h | h |
The basic rating life in operating hours, that is reached or exceeded by 90% of a sufficiently large number of apparently identical bearings before the first indications of material fatigue appear |
| C | N |
Basic dynamic load rating, see product tables |
| P | N |
Equivalent dynamic bearing load |
| p | - |
Life exponent; for roller bearings: p = 10/3 for ball bearings: p = 3 |
| n | min-1 |
Operating speed (nominal speed) |
Equivalent dynamic bearing load
The basic rating life L10 in accordance with ➤ Equation is defined for a load of constant magnitude acting in a constant direction. In the case of radial bearings, this is a purely radial load, while in the case of axial bearings it is a purely axial load.
Equivalent dynamic load P is identical to the combined load occurring in practice
If the load and speed are not constant, equivalent operating values can be determined that induce the same fatigue as the actual loading conditions.
Equivalent operating values for variable load and speed ➤ section.
Equivalent dynamic radial bearing load
The equivalent dynamic load P on a bearing subjected to combined load (with a radial and axial load) is calculated in accordance with ➤ Equation.
Equivalent dynamic radial bearing load
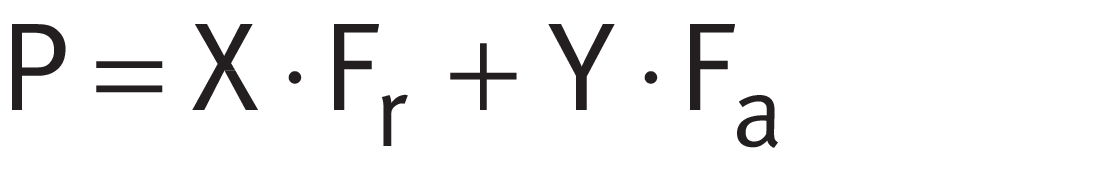
Legend
| P | N |
Equivalent dynamic radial bearing load |
| X | - |
Radial load factor; see product tables |
| Fr | N |
Radial load |
| Y | - |
Axial load factor; see product tables |
| Fa | N |
Axial load |
The calculation in accordance with ➤ Equation cannot be applied to radial needle roller bearings, axial needle roller bearings and axial cylindrical roller bearings. Combined loads are not permissible with these bearings.
For radial needle roller bearings ➤ Equation, for axial bearings ➤ Equation.
Equivalent dynamic radial bearing load

Legend
| P | N |
Equivalent dynamic radial bearing load |
| Fr | N |
Radial load |
Equivalent dynamic axial bearing load
In axial bearings with α = 90°, only axial loads are possible
Axial deep groove ball bearings, axial cylindrical roller bearings, axial needle roller bearings and axial tapered roller bearings with the nominal contact angle α = 90° can only support purely axial forces. For concentric axial load ➤ Equation.
Equivalent dynamic axial bearing load
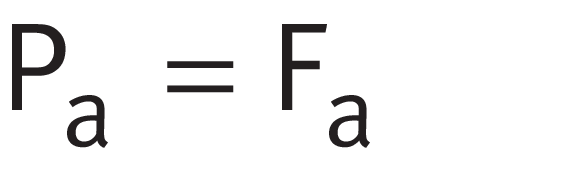
Legend
| Pa | N |
Equivalent dynamic axial bearing load |
| Fa | N |
Axial load |
In axial bearings with α ≠ 90°, axial and radial loads are possible
Axial angular contact ball bearings, axial spherical roller bearings and axial tapered roller bearings with the nominal contact angle α ≠ 90° can support not only an axial force Fa but also a radial force Fr. The equivalent dynamic axial load Pa is thus determined in accordance with ➤ Equation.
Equivalent dynamic axial bearing load
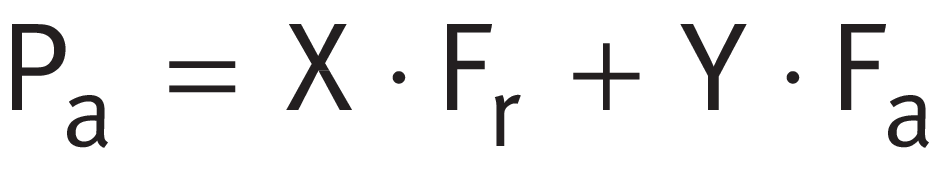
Legend
| Pa | N |
Equivalent dynamic axial bearing load |
| X | - |
Radial load factor; see product tables |
| Fr | N |
Radial load |
| Y | - |
Axial load factor; see product tables |
| Fa | N |
Axial load |
Expanded adjusted rating life
The calculation of the expanded adjusted rating life Lnm was standardised for the first time in DIN ISO 281 Appendix 1 and included in the global standard ISO 281 in 2007. It replaces the previously used adjusted rating life Lna. Computer-aided calculation to DIN ISO 281 Appendix 4 has been specified since 2008 in ISO/TS 16281 and standardised in DIN 26281 since 2010.
The expanded adjusted rating life Lnm is calculated in accordance with ➤ Equation.
Expanded adjusted rating life
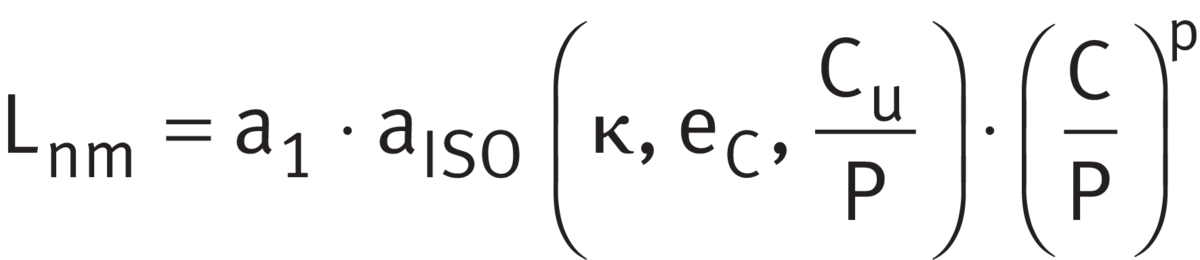
Legend
| Lnm | 106 |
Expanded adjusted rating life in millions of revolutions in accordance with ISO 281:2007 |
| a1 | - |
Life adjustment factor for a requisite reliability other than 90% ➤ Table |
| aISO | - |
Life adjustment factor for operating conditions |
| κ | - |
Viscosity ratio |
| eC | - |
Life adjustment factor for contamination |
| Cu | kN |
Fatigue limit load; see product tables |
| C | kN |
Basic dynamic load rating; see product tables |
| P | kN |
Equivalent dynamic bearing load |
| p | - |
Life exponent |
Fatigue limit load Cu
The fatigue limit load Cu in accordance with ISO 281 is defined as the load below which, under laboratory conditions, no fatigue occurs in the material. The fatigue limit load Cu serves as a calculation value for determining the life adjustment factor aISO and not as a design criterion. With poor lubrication or contamination of the lubricant in particular, it is also possible for the material to undergo fatigue at loads which are significantly below the fatigue limit load Cu.
Life adjustment factor a1
The values for the life adjustment factor a1 were redefined in ISO 281:2007 and differ from the previous data ➤ Table.
Life adjustment factor a1
|
Requisite reliability |
Expanded adjusted |
Life adjustment factor |
|---|---|---|
|
% |
Lnm |
a1 |
|
90 |
L10m |
1 |
|
95 |
L5m |
0,64 |
|
96 |
L4m |
0,55 |
|
97 |
L3m |
0,47 |
|
98 |
L2m |
0,37 |
|
99 |
L1m |
0,25 |
|
99,2 |
L0,8m |
0,22 |
|
99,4 |
L0,6m |
0,19 |
|
99,6 |
L0,4m |
0,16 |
|
99,8 |
L0,2m |
0,12 |
|
99,9 |
L0,1m |
0,093 |
|
99,92 |
L0,08m |
0,087 |
|
99,94 |
L0,06m |
0,08 |
|
99,95 |
L0,05m |
0,077 |
Life adjustment factor aISO
Influences on the life adjustment factor
The standardised method for calculating the life adjustment factor aISO essentially takes account of:
- the load on the bearing
- the lubrication conditions (viscosity and type of lubricant, speed, bearing size, additives)
- the fatigue limit of the material
- the type of bearing
- the residual stress in the material
- the environmental conditions
- contamination of the lubricant
Life adjustment factor for operating conditions
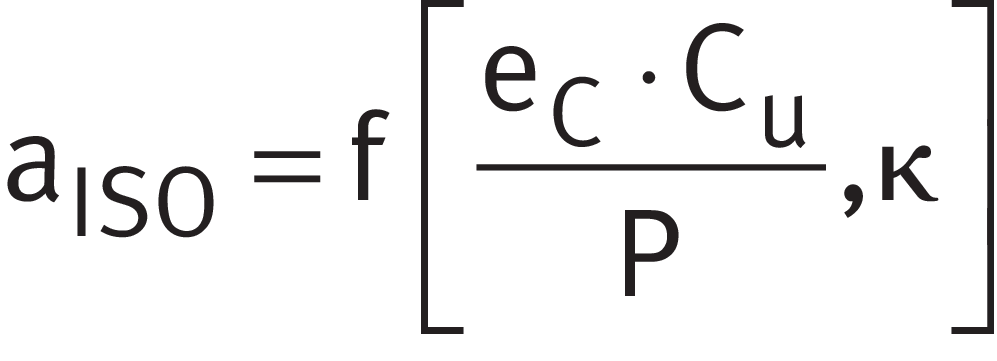
Legend
| aISO | - |
Life adjustment factor for operating conditions ➤ Figure to ➤ Figure |
| eC | - |
Life adjustment factor for contamination ➤ Table |
| Cu | N |
Fatigue limit load; see product tables |
| P | N |
Equivalent dynamic bearing load |
| κ | - |
Viscosity ratio ➤ link For κ > 4 calculation should be carried out using κ = 4. This calculation method cannot be used for κ < 0,1 |
Taking account of EP additives in the lubricant
In accordance with ISO 281, EP additives in the lubricant can be taken into consideration in the following way:
- For a viscosity ratio κ < 1 and a contamination factor eC ≧ 0,2, calculation can be carried out using the value κ = 1 for lubricants with EP additives that have proven effective. Under severe contamination (contamination factor eC < 0,2), the effectiveness of the additives under these contamination conditions must be demonstrated. The effectiveness of the EP additives can be demonstrated in the actual application or on a rolling bearing test rig FE8 to DIN 51819-1.
- If the EP additives are proven effective and calculation is carried out using the value κ = 1, the life adjustment factor must be restricted to aISO ≦ 3. If the value aISO calculated for the actual value κ is greater than 3, this value can be used in calculation
For practical purposes, the life adjustment factor should be restricted to aISO ≦ 50. This limit value also applies if eC · Cu/P > 5. For a viscosity ratio κ > 4, the value κ = 4 should be used; if κ < 0,1, the calculation is not valid.
The life adjustment factor aISO can – depending on the bearing type – be determined from ➤ Figure to ➤ Figure.
|
Life adjustment factor aISO for radial roller bearings aISO = life adjustment factor Cu = fatigue limit load eC = contamination factor P = equivalent dynamic bearing load κ = parameter for the lubrication regime (viscosity ratio) |
 |
|
Life adjustment factor aISO for axial roller bearings aISO = life adjustment factor Cu = fatigue limit load eC = contamination factor P = equivalent dynamic bearing load κ = parameter for the lubrication regime (viscosity ratio) |
 |
|
Life adjustment factor aISO for radial ball bearings aISO = life adjustment factor Cu = fatigue limit load eC = contamination factor P = equivalent dynamic bearing load κ = parameter for the lubrication regime (viscosity ratio) |
 |
|
Life adjustment factor aISO for axial ball bearings aISO = life adjustment factor Cu = fatigue limit load eC = contamination factor P = equivalent dynamic bearing load κ = parameter for the lubrication regime (viscosity ratio) |
 |
Viscosity ratio κ
The viscosity ratio κ is an indication of the quality of lubricant film formation ➤ Equation.
Viscosity ratio
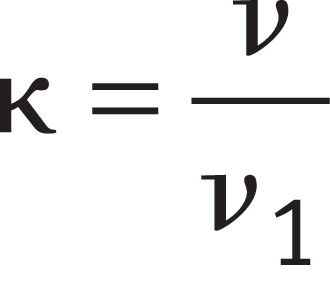
Legend
| κ | - |
Viscosity ratio |
| ν | mm2/s |
Kinematic viscosity of the lubricant at operating temperature |
| ν1 | mm2/s |
Reference viscosity of the lubricant at operating temperature |
Reference viscosity
The reference viscosity ν1 is determined from the mean bearing diameter dM = (D + d)/2 and the operating speed n ➤ Figure.
Nominal viscosity
The nominal viscosity of the oil at +40 °C is determined from the required operating viscosity ν and the operating temperature ϑ, ➤ Figure. In the case of greases, ν is the operating viscosity of the base oil.
In the case of heavily loaded bearings with a high proportion of sliding contact, the temperature in the contact area of the rolling elements may be up to 20 K higher than the temperature measured on the stationary ring (without the influence of any external heat sources).
Taking account of EP additives in calculation of the expanded adjusted rating life Lnm ➤ link.
ν1 for n < 1 000 min-1 or n ≧ 1 000 min-1
The reference viscosity ν1 is calculated for n < 1 000 min-1 in accordance with ➤ Equation, for n ≧ 1 000 min-1 in accordance with ➤ Equation. By differentiating between these cases, the effect of starvation at high speeds is taken into account.
Reference viscosity
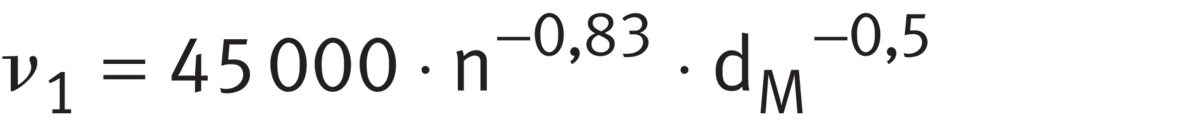
Reference viscosity
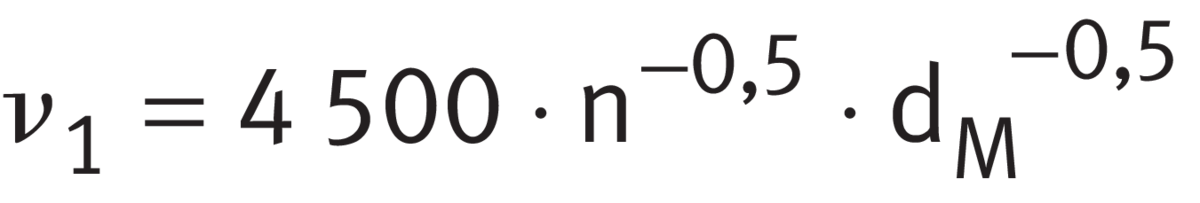
Legend
| ν1 | mm2/s |
Reference viscosity of the lubricant at operating temperature |
| n | min-1 |
Operating speed |
| dM | mm |
Mean bearing diameter dM = (D + d)/2 |
ν1 for synthetic oils
In accordance with ISO 281:2007, the equations ➤ Equation and ➤ Equation can also be used in approximate terms for synthetic oils, such as oils based on synthetic hydrocarbons (SHC) for example.
|
Reference viscosity ν1 ν1 = reference viscosity dM = mean bearing diameter; (d + D)/2 n = operating speed |
 |
|
ν/ϑ diagram for mineral oils ν = operating viscosity ϑ = operating temperature ν40 = viscosity at +40 °C |
 |
Life adjustment factor for contamination
Contamination factor eC
The life adjustment factor for contamination eC takes account of the influence of contamination in the lubrication gap on the rating life ➤ Table.
The rating life is reduced by solid particles in the lubrication gap and is dependent on:
- the type, size, hardness and number of particles
- the relative lubrication film thickness
- the bearing size
Due to the complex interactions between these influencing factors, it is only possible to give approximate guide values. The values in the tables are valid for contamination by solid particles (factor eC). No account is taken of other contamination such as that caused by water or other fluids. Under severe contamination (eC → 0) the bearings may fail due to wear. In this case, the operating life is substantially less than the calculated life.
➤ Table shows guide values for the contamination factor eC. The values are given in DIN ISO 281. An aid to selecting the appropriate cleanliness class is given in DIN ISO 281 Appendix 3. This appendix also gives guidance on achieving the individual cleanliness classes.
Guide values for the contamination factor eC
|
Contamination |
Contamination factor eC |
|||
|---|---|---|---|---|
|
dM < 100 mm |
dM ≧ 100 mm |
|||
|
from |
to |
from |
to |
|
|
Very high cleanliness:
|
1 |
1 |
||
|
High cleanliness:
|
0,8 |
0,6 |
0,9 |
0,8 |
|
Standard cleanliness:
|
0,6 |
0,5 |
0,8 |
0,6 |
|
Slight contamination:
|
0,5 |
0,3 |
0,6 |
0,4 |
|
Typical contamination:
|
0,3 |
0,1 |
0,4 |
0,2 |
|
Heavy contamination:
|
0,1 |
0 |
0,1 |
0 |
|
Very heavy contamination |
0 |
0 |
||
dM = mean bearing diameter (d + D)/2
Requisite minimum load
In order to prevent damage due to slippage, a minimum radial or axial load must be applied to the bearings ➤ Table.
Recommended minimum radial and axial load for rolling bearings
|
Bearing type |
Recommended minimum load |
|---|---|
|
Deep groove ball bearings |
P > C0 /100 |
|
Angular contact ball bearings |
P > C0 /100 |
|
Self-aligning ball bearings |
P > C0 /100 |
|
Cylindrical roller bearings |
P > C0 /60 |
|
Tapered roller bearings |
P > C0 /60 |
|
Barrel roller bearings |
P > C0 /60 |
|
Spherical roller bearings |
P > C0 /100 |
|
Toroidal roller bearings, |
P > C0 /75 |
|
Needle roller bearings |
P > C0 /60 |
|
Axial deep groove ball bearings |
|
|
Axial cylindrical roller bearings 1) |
|
|
Axial needle roller bearings |
|
|
Axial spherical roller bearings2) |
|
Factor ka for axial cylindrical roller bearings
|
Series |
Factor ka |
|---|---|
|
K811 |
1,4 |
| K812 | 0,9 |
| K893 | 0,7 |
| K894 | 0,5 |
Factor ka for axial spherical roller bearings
|
Series |
Factor ka |
|---|---|
|
292..-E |
0,6 |
|
293..-E1(E) |
0,9 |
|
294..-E1(E) |
0,7 |
Equivalent operating values
Equivalent operating values for non-constant loads and speeds
The rating life equations assume a constant bearing load P and constant bearing speed n. If the load and speed are not constant, equivalent operating values can be determined that induce the same fatigue as the actual loading conditions.
The operating values calculated here already take account of the life adjustment factors aISO. They must not be applied again when calculating the adjusted rating life.
Variable load and speed
If the load and speed vary over a time period T, the speed n and the equivalent bearing load P ➤ Equation and ➤ Equation are calculated as follows. If only a basic rating life is to be calculated, the terms 1/aISO can be omitted from the equations ➤ Equation to ➤ Equation.
Equivalent speed
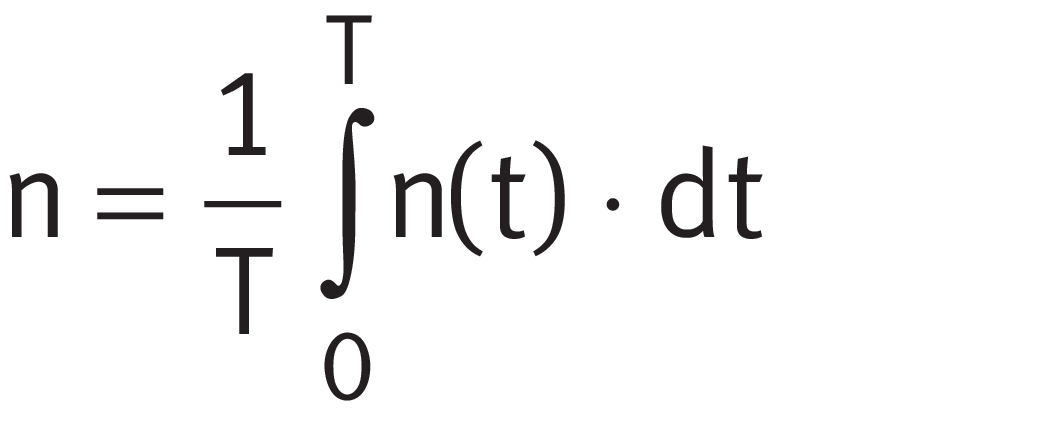
Equivalent bearing load
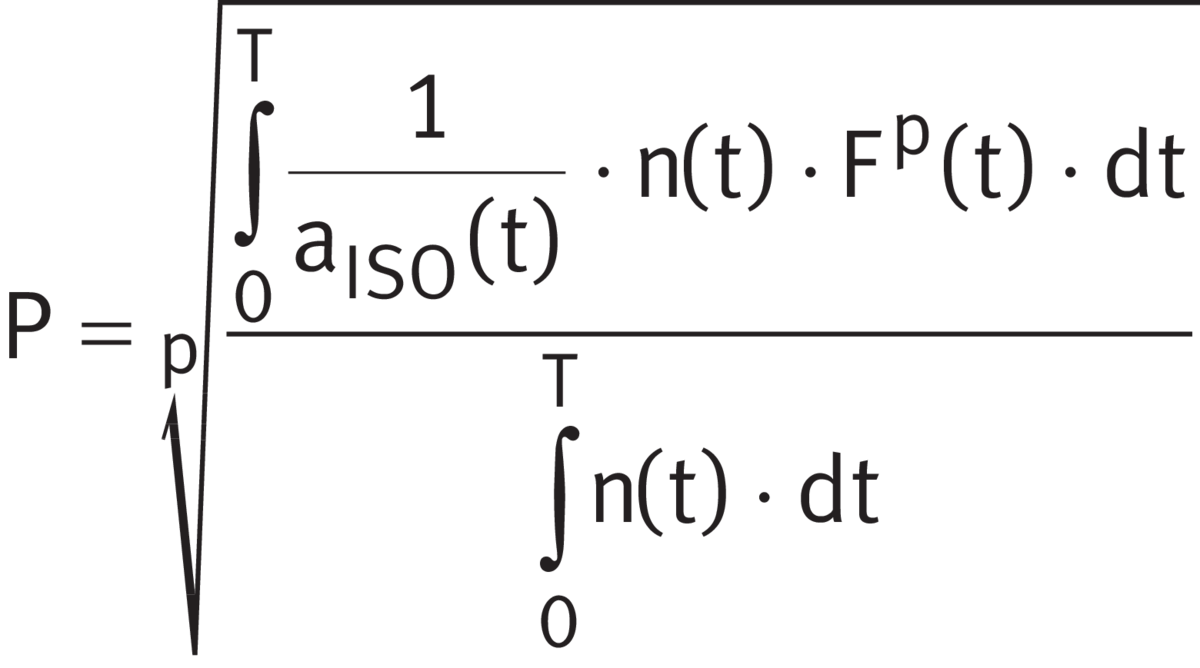
Variation in steps
If the load and speed vary in steps over a time period T, n and P are calculated as follows ➤ Equation and ➤ Equation.
Equivalent speed
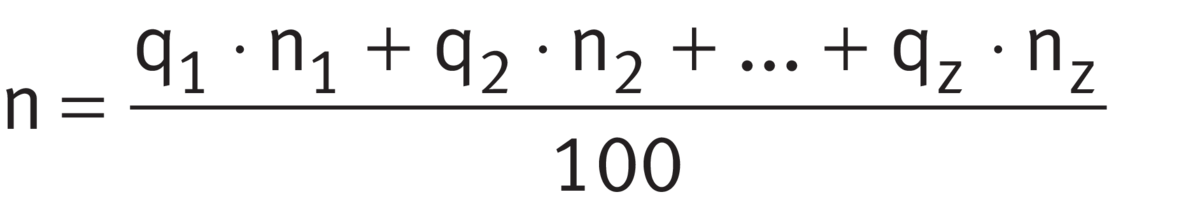
Equivalent bearing load
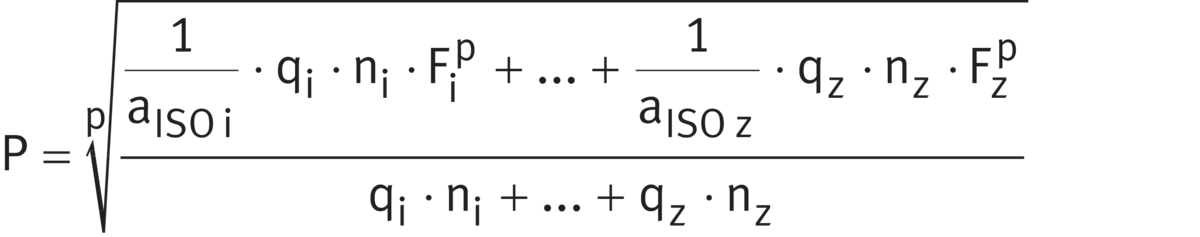
Variable load at constant speed
If the function F describes the variation in the load over a time period T and the speed is constant, P is calculated as follows ➤ Equation.
Equivalent bearing load
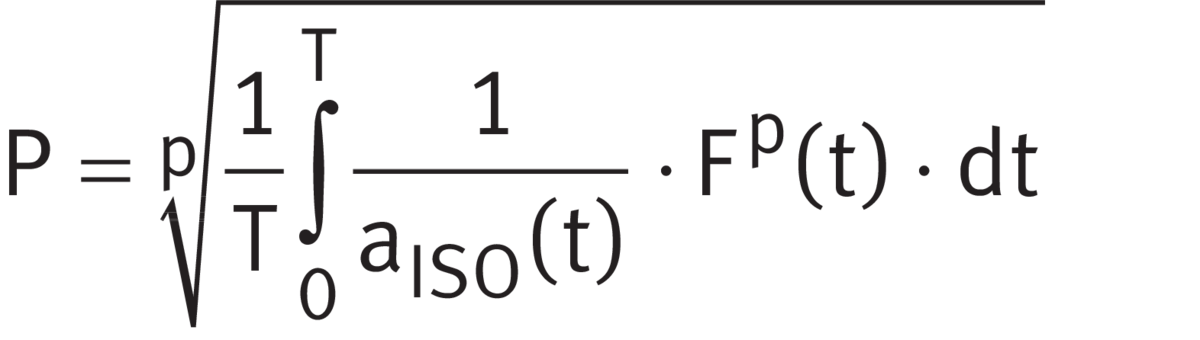
Load varying in steps at constant speed
If the load varies in steps over a time period T and the speed is constant, P is calculated as follows ➤ Equation.
Equivalent bearing load
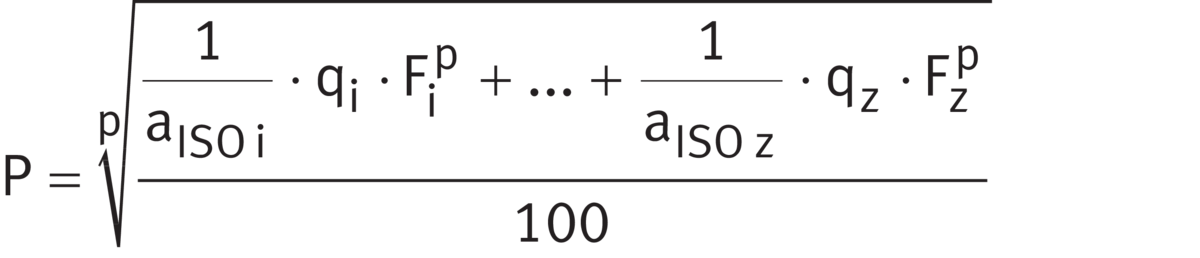
Constant load at variable speed
If the speed varies but the load remains constant, the following applies ➤ Equation.
Equivalent speed
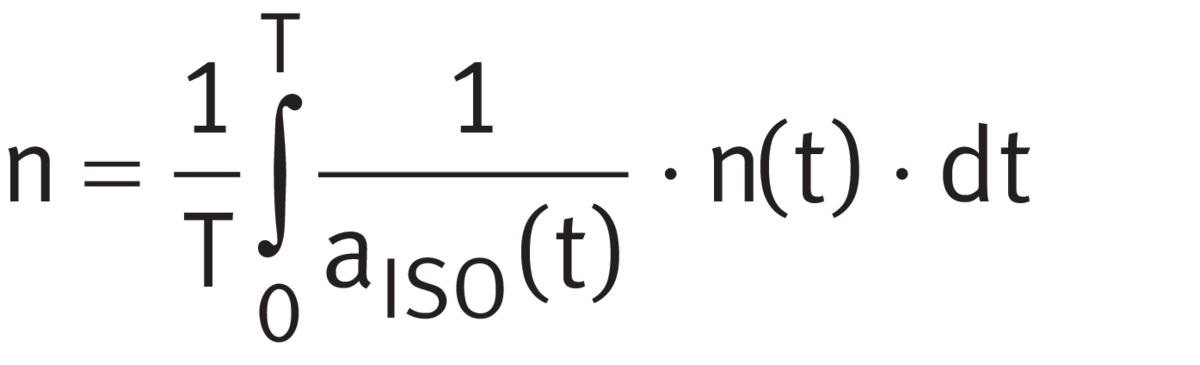
Constant load with speed varying in steps
If the speed varies in steps, the following applies ➤ Equation.
Equivalent speed
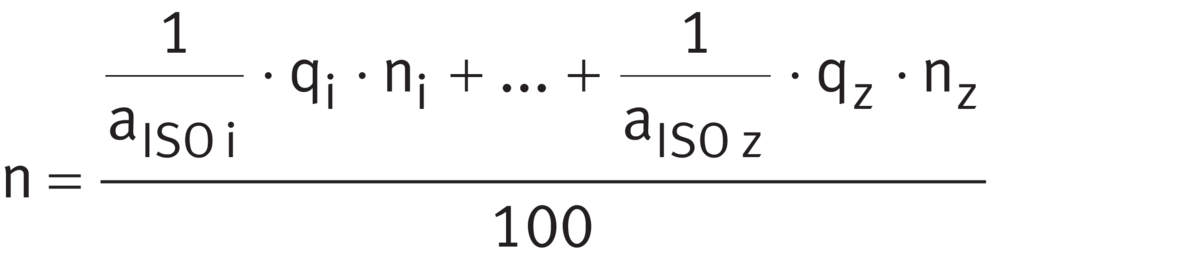
Swivel motion
The equivalent speed is calculated in accordance with ➤ Equation.

If the swivel angle is smaller than twice the pitch angle of the rolling elements, there is a risk of false brinelling.
Equivalent speed
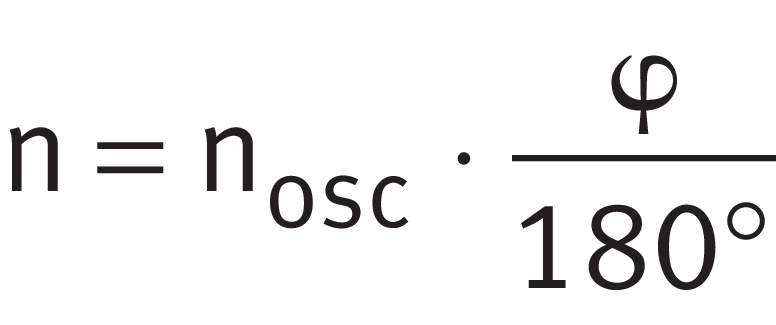
Legend
| n | min-1 |
Equivalent speed |
| T | min |
Time period under consideration |
| P | N |
Equivalent bearing load |
| p | - |
Life exponent; |
| aISO i, aISO(t) |
- |
Life adjustment factor aISO for current operating condition |
| ni, n(t) | min-1 |
Bearing speed for current operating condition |
| qi | % |
Duration of operating condition as a proportion of the total operating period; |
| Fi, F(t) | N |
Bearing load during the current operating condition |
| nosc | min-1 |
Frequency of swivel motion |
| φ | ° |
Swivel angle ➤ Figure |
|
Swivel motion, swivel angle Complete swivel motion = 2 · φs φs = swivel angle of the bearing φa = swivel angle at which every point on the outer raceway is overrolled |
 |
Guide values for dimensioning
Guide values for rating life
The values for the recommended rating life are guide values for normal operating conditions ➤ Table to ➤ Table. In addition, the tables give the operating life values that are usually achieved in practice at various mounting locations.
Do not overspecify the bearings, otherwise it may not be possible to observe the requisite minimum load. Recommended minimum load ➤ section and product chapter.
Motor vehicles
|
Mounting location |
Recommended rating life |
|||
|---|---|---|---|---|
|
h |
||||
|
Ball bearings |
Roller bearings |
|||
|
from |
to |
from |
to |
|
|
Motorcycles |
400 |
2 000 |
400 |
2 400 |
|
Passenger car powertrains |
500 |
1 100 |
500 |
1 200 |
|
Passenger car gearboxes |
200 |
500 |
200 |
500 |
|
Passenger car wheel bearings |
1400 |
5 00 |
1 500 |
7 000 |
|
Light commercial vehicles |
2 000 |
4 000 |
2 400 |
5 000 |
|
Medium commercial vehicles |
2 900 |
5 300 |
3 600 |
7 000 |
|
Heavy commercial vehicles |
4 000 |
8 800 |
5 000 |
12 000 |
|
Buses |
2 900 |
11 000 |
3 600 |
16 000 |
|
Internal combustion engines |
900 |
4 000 |
900 |
5 000 |
Rail vehicles
|
Mounting location |
Operating life |
|
|---|---|---|
|
Millions of kilometres |
||
|
from |
to |
|
|
Wheelset bearings for freight wagons |
0,1 |
0,1 |
|
Urban transport vehicles |
1 |
2 |
|
Passenger carriages |
2 |
3 |
|
Goods wagons |
1 |
2 |
|
Tipper wagons |
1 |
2 |
|
Powered units |
2 |
3 |
|
Locomotives, external bearings |
2 |
4 |
|
Locomotives, internal bearings |
2 |
4 |
|
Shunting and industrial locomotives |
0,5 |
1 |
|
Gearboxes for rail vehicles |
0,5 |
2 |
Shipbuilding
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Marine thrust bearings |
‒ |
‒ |
20 000 |
50 000 |
30 000 |
80 000 |
|
Marine shaft bearings |
‒ |
‒ |
50 000 |
200 000 |
30 000 |
80 000 |
|
Large marine gearboxes |
14 000 |
46 000 |
20 000 |
75 000 |
30 000 |
80 000 |
|
Small marine gearboxes |
4 000 |
14 000 |
5 000 |
20 000 |
5 000 |
20 000 |
|
Boat propulsion systems |
1 700 |
7 800 |
2 000 |
10 000 |
2 000 |
10 000 |
Agricultural machinery
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Tractors |
1 700 |
4 000 |
2 000 |
5 000 |
5 000 |
10 000 |
|
Self-propelled machinery |
1 700 |
4 000 |
2 000 |
5 000 |
2 000 |
6 000 |
|
Seasonal machinery |
500 |
1 700 |
500 |
2 000 |
500 |
2 000 |
Construction machinery
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Dozers, loaders |
4 000 |
7800 |
5 000 |
10 000 |
5 000 |
10 000 |
|
Excavators, |
500 |
1 700 |
500 |
2 000 |
500 |
2 000 |
|
Excavators, slewing gear |
1 700 |
4 000 |
2 000 |
5 000 |
2 000 |
5 000 |
|
Vibratory road rollers, |
1 700 |
4 000 |
2 000 |
5 000 |
5 000 |
30 000 |
|
Vibrator bodies |
500 |
1 700 |
500 |
2 000 |
500 |
2 000 |
Electric motors
|
Mounting location |
Recommended rating life |
Operating life |
|||||
|---|---|---|---|---|---|---|---|
|
h |
h |
||||||
|
Ball bearings |
Roller bearings |
||||||
|
from |
to |
from |
to |
from |
to |
||
|
Electric motors |
1 700 |
4 000 |
‒ |
‒ |
500 |
1000 |
|
|
Series motors |
21 000 |
32 000 |
35 000 |
50 000 |
20 000 |
30 000 |
|
|
Large motors |
32 000 |
63 000 |
50 000 |
110 000 |
40 000 |
50 000 |
|
|
Wind energy generators |
‒ |
‒ |
‒ |
‒ |
100 000 |
200 000 |
|
|
Generators |
‒ |
‒ |
‒ |
‒ |
40 000 |
50 000 |
|
|
continued ▼ |
|||||||
Electric motors
| Mounting location |
Recommended rating life |
Operating life |
|||||
|---|---|---|---|---|---|---|---|
|
h |
km |
||||||
|
Ball bearings |
Roller bearings |
||||||
|
from |
to |
from |
to |
from |
to |
||
| Electric traction motors for | 14 000 | 21 000 | 20 000 | 35 000 | ‒ | ||
| mainline operations |
‒ |
‒ |
‒ |
‒ |
2 000 000 |
2 500 000 |
|
| trams |
‒ |
‒ |
‒ |
‒ |
1000 000 |
1000 000 |
|
| suburban and underground trains |
‒ |
‒ |
‒ |
‒ |
1500 000 |
1500 000 |
|
|
continued ▲ |
|||||||
Rolling mills, steelworks equipment
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Rolling mill frames |
500 |
14 000 |
500 |
20 000 |
2 000 |
10 000 |
|
Rolling mill gearboxes |
14 000 |
32 000 |
20 000 |
50 000 |
20 000 |
40 000 |
|
Roller tables |
7 800 |
21 000 |
10 000 |
35 000 |
20 000 |
40 000 |
|
Centrifugal casting machines |
21 000 |
46 000 |
35 000 |
75 000 |
30 000 |
60 000 |
Machine tools
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Headstock spindles, |
14 000 |
46 000 |
20 000 |
75 000 |
10 000 |
30 000 |
|
Drilling spindles |
14 000 |
32 000 |
20 000 |
50 000 |
1 000 |
20 000 |
|
External grinding spindles |
7 800 |
21 000 |
10 000 |
35 000 |
10 000 |
20 000 |
| Hole grinding spindles | ‒ | 500 | 2 000 | |||
|
Workpiece spindles |
21 000 |
63 000 |
35 000 |
110 000 |
20 000 |
30 000 |
|
Machine tool gearboxes |
14 000 |
32 000 |
20 000 |
50 000 |
10 000 |
20 000 |
|
Presses, flywheels |
21 000 |
32 000 |
35 000 |
50 000 |
20 000 |
30 000 |
|
Presses, eccentric shafts |
14 000 |
21 000 |
20 000 |
35 000 |
10 000 |
20 000 |
|
Electric tools and |
4 000 |
14 000 |
5 000 |
20 000 |
100 |
200 |
Woodworking machinery
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Milling spindles and cutter blocks |
14 000 |
32 000 |
20 000 |
50 000 |
10 000 |
20 000 |
| Saw frames, main bearings |
‒ | ‒ | 35 000 | 35 000 | ‒ | |
| Saw frames, connecting rod bearings |
‒ | ‒ | 10 000 | 20 000 | ‒ | |
|
Circular saws |
4 000 |
14 000 |
5 000 |
20 000 |
10 000 |
20 000 |
Gearboxes in general machine building
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Universal gearboxes |
4 000 |
14 000 |
5 000 |
20 000 |
5 000 |
20 000 |
|
Geared motors |
4 000 |
14 000 |
5 000 |
20 000 |
5 000 |
20 000 |
|
Large gearboxes, |
14 000 |
46 000 |
20 000 |
75 000 |
20 000 |
80 000 |
Conveying equipment
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Belt drives, |
‒ |
‒ |
75 000 |
150 000 |
10 000 |
30 000 |
|
Conveyor belt rollers, |
46 000 |
63 000 |
75 000 |
110 000 |
10 000 |
30 000 |
|
Conveyor belt rollers, |
7 800 |
21000 |
10 000 |
35 000 |
10 000 |
30 000 |
|
Belt drums |
‒ |
‒ |
50 000 |
75 000 |
10 000 |
30 000 |
|
Bucket wheel excavators, |
7 800 |
21 000 |
10 000 |
35 000 |
5 000 |
15 000 |
|
Bucket wheel excavators, |
‒ |
‒ |
75 000 |
200 000 |
30 000 |
50 000 |
|
Bucket wheel excavators, |
46 000 |
83 000 |
75 000 |
150 000 |
30 000 |
50 000 |
|
Winding cable sheaves |
32 000 |
46 000 |
50 000 |
75 000 |
50 000 |
80 000 |
|
Sheaves |
7 800 |
21 000 |
10 000 |
35 000 |
8 000 |
30 000 |
|
Tunnel-boring machines: |
‒ |
‒ |
‒ |
‒ |
5 000 |
10 000 |
Pumps, fans, compressors
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Ventilators, fans |
21 000 |
46 000 |
35 000 |
75 000 |
20 000 |
100 000 |
|
Large fans |
32 000 |
63 000 |
50 000 |
110 000 |
>10 000 |
|
|
Piston pumps |
21 000 |
46 000 |
35 000 |
75 000 |
20 000 |
50 000 |
|
Centrifugal pumps |
14 000 |
46 000 |
20 000 |
75 000 |
20 000 |
50 000 |
|
Hydraulic axial and |
500 |
7 800 |
500 |
10 000 |
1 000 |
20 000 |
|
Gear pumps |
500 |
7 800 |
500 |
10 000 |
1 000 |
20 000 |
|
Compressors |
4 000 |
21 000 |
5 000 |
35 000 |
30 000 |
80 000 |
Centrifuges, stirrers
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Centrifuges |
7 800 |
14 000 |
10 000 |
20 000 |
40 000 |
60 000 |
|
Large stirrers |
21 000 |
32 000 |
35 000 |
50 000 |
40 000 |
50 000 |
Textile machinery
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Spinning machines, |
21 000 |
46 000 |
35 000 |
75 000 |
10 000 |
50 000 |
|
Weaving and |
14 000 |
32 000 |
20 000 |
50 000 |
10 000 | 50 000 |
Plastics processing
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Plastics worm extruders |
14 000 |
21 000 |
20 000 |
35 000 |
20 000 |
100 000 |
|
Rubber and |
21 000 |
46 000 |
35 000 |
75 000 |
20 000 | 100 000 |
Crushers, mills, screens
|
Mounting location |
Recommended rating life |
Operating life |
||||
|---|---|---|---|---|---|---|
|
h |
h |
|||||
|
Ball bearings |
Roller bearings |
|||||
|
from |
to |
from |
to |
from |
to |
|
|
Jaw crushers |
‒ |
‒ |
20 000 |
35 000 |
25 000 |
40 000 |
|
Gyratory crushers, |
‒ |
‒ |
20 000 |
35 000 |
25 000 | 40 000 |
|
Rigid hammer mills, |
‒ | ‒ |
50 000 |
110 000 |
40 000 |
40 000 |
|
Tube mills |
‒ |
‒ |
50 000 |
100 000 |
100 000 |
100 000 |
|
Vibration grinding mills |
‒ |
‒ |
5 000 |
20 000 |
30 000 |
60 000 |
|
Grinding track mills |
‒ |
‒ |
50 000 |
110 000 |
60 000 |
100 000 |
|
Vibrating screens |
‒ |
‒ |
10 000 |
20 000 |
10 000 |
30 000 |
|
Briquette presses |
‒ |
‒ |
35 000 |
50 000 |
40 000 |
40 000 |
|
Rotary kiln radial |
‒ |
‒ |
50 000 |
110 000 |
> |
100 000 |
|
Roller presses |
‒ |
‒ |
‒ |
‒ |
40 000 |
40 000 |
Paper and printing machinery
|
Mounting location |
Recommended rating life |
Operating life |
|||||
|---|---|---|---|---|---|---|---|
|
h |
h |
||||||
|
Ball bearings |
Roller bearings |
||||||
|
from |
to |
from |
to |
from |
to |
||
|
Paper machinery, |
‒ |
‒ |
110 000 |
150 000 |
50 000 |
100 000 |
|
| Paper machinery, dry section |
‒ | ‒ | 150 000 | 250 000 | ‒ | ||
| Guide rolls | 50 000 | 120 000 | 150 000 | 250 000 | ‒ | ||
| Dryer rolls | 50 000 | 150 000 | 150 000 | 250 000 | ‒ | ||
| M.G. cylinders | 50 000 | 200 000 | 150 000 | 250 000 | ‒ | ||
|
Paper machinery, |
‒ |
‒ |
80 000 |
120 000 |
50 000 |
100 000 |
|
|
Paper machinery, |
‒ |
‒ |
80 000 |
110 000 |
50 000 |
100 000 |
|
|
Printing machinery |
32 000 |
46 000 |
50 000 |
75 000 |
30 000 |
60 000 |
|
Static load carrying capacity
Plastic deformation limits the static load carrying capacity
If high, static or shock loads occur, the raceways and rolling elements may undergo plastic deformation. This deformation limits the static load carrying capacity of the rolling bearing with respect to the permissible noise level during operation of the bearing.
Basic static load rating
If a rolling bearing operates with only infrequent rotary motion or completely without rotary motion, its size is determined in accordance with the basic static load rating C0.
In accordance with DIN ISO 76, this is:
- a constant radial load C0r for radial bearings
- a constant, concentrically acting axial load C0a for axial bearings
The basic static load rating C0 is that load under which the Hertzian pressure at the most heavily loaded point between the rolling elements and raceways reaches the following values:
- for roller bearings, 4 000 N/mm2
- for ball bearings, 4 200 N/mm2
- for self-aligning ball bearings, 4 600 N/mm2
Under normal contact conditions, this load causes a permanent deformation at the contact points of approx. 1/10 000 of the rolling element diameter.
Static load safety factor
In addition to dimensioning on the basis of the fatigue life, it is advisable to check the static load safety factor. Guide values and shock loads occurring during operation in accordance with ➤ Table must be taken into consideration.
Static load safety factor
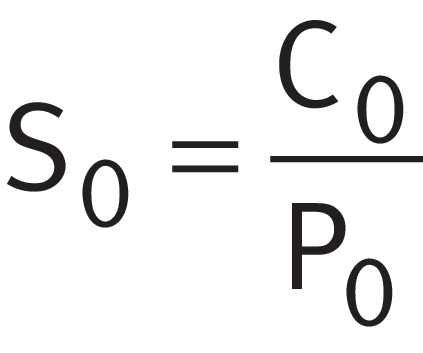
Legend
| S0 | - |
Static load safety factor; guide values ➤ Table |
| C0r, C0a | N |
Basic radial or axial static load rating; see product tables |
| P0r, P0a | N |
Radial or axial equivalent static bearing load ➤ Equation |
Guide values for static load safety factor
Guide values for the requisite static load safety factor S0 are given in DIN ISO 76:2009-01 and in ➤ Table. Guide values for axial spherical roller bearings and high precision bearings: see corresponding product description. For drawn cup needle roller bearings, S0 ≧ 3 is necessary.
Static load safety factor S0 for ball and roller bearings – guide values
|
Operating conditions and application |
Static load safety factor S0 |
|
|---|---|---|
|
min. |
||
|
Ball bearings |
Roller bearings |
|
|
Low-noise, smooth running, free from vibrations, high rotational accuracy |
2 |
3 |
|
Normal, smooth running, free from vibrations, normal rotational accuracy |
1 |
1,5 |
|
Pronounced shock loading1) |
1,5 |
3 |
- If the order of magnitude of the shock loading is not known, the values used for S0 should be at least 1,5. If the order of magnitude of the shock loading is known precisely, lower values are possible.
Equivalent static bearing load
The equivalent static load P0 is a calculated value. It corresponds to a radial load in radial bearings and a concentric axial load in axial bearings.
P0 induces the same load at the centre point of the most heavily loaded contact point between the rolling element and raceway as the combined load occurring in practice.
Equivalent static bearing load

Legend
| P0 | N |
Equivalent static bearing load |
| X0 | N |
Radial load factor; see product tables or product description |
| Fr, Fa | N |
Largest radial or axial load present |
| Y0 | N |
Axial load factor; see product tables or product description |
The calculation cannot be applied to radial needle roller bearings, axial needle roller bearings and axial cylindrical roller bearings. Combined loads are not permissible with these bearings.
For axial needle roller bearings and axial cylindrical roller bearings: P0 = F0a.
Operating life
The operating life is defined as the life actually achieved by the bearing. It may differ significantly from the calculated life.
Possible factors influencing the operating life
This may be due to wear or fatigue as a result of:
- deviating operating data
- misalignments between the shaft and housing
- insufficient or excessive operating clearance
- contamination
- insufficient lubrication
- excessive operating temperature
- oscillating bearing movement with very small swivel angles (false brinelling)
- high vibration and false brinelling
- very high shock loads (static overloading)
- prior damage during mounting
The operating life cannot be calculated
Due to the wide variety of possible installation and operating conditions, it is not possible to precisely predetermine the operating life. The most reliable way of arriving at a close estimate is by comparison with similar applications.



